In the previous post, we discussed the two properties of ACID, Atomocity and Consistency.
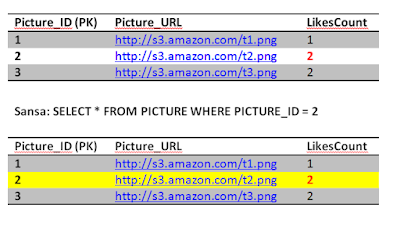
Brief recap, the Picture table has the LikesCount field which keeps track of how many likes a picture got. This is a performance tweak in order to avoid querying the Like table every time we want to get the likes count for a picture. We notice that picture 1 has 1 like only by Jon and picture 3 has two likes by Reek and Sansa. Picture 2 has 1 like by Jon. The Picture_ID is the primary key in the Picture table, while both the Picture_ID and the User constitute the primary key for the Like table. There are many fields that we can add but for simplicity we are sticking with these now.
This is how our tables look like after the last post.
Here is the reference to all ACID posts that I authored:
ACID (Part 1) - Atomicity and Consistency
ACID (Part 2) - Isolation (Read Uncommitted)
ACID (Part 3) - Isolation (Read Committed)
ACID (Part 4) - Isolation (Repeatable Read)
There are four types of isolation levels that we will try to cover.
Brief recap, the Picture table has the LikesCount field which keeps track of how many likes a picture got. This is a performance tweak in order to avoid querying the Like table every time we want to get the likes count for a picture. We notice that picture 1 has 1 like only by Jon and picture 3 has two likes by Reek and Sansa. Picture 2 has 1 like by Jon. The Picture_ID is the primary key in the Picture table, while both the Picture_ID and the User constitute the primary key for the Like table. There are many fields that we can add but for simplicity we are sticking with these now.
ACID (Part 1) - Atomicity and Consistency
ACID (Part 2) - Isolation (Read Uncommitted)
ACID (Part 3) - Isolation (Read Committed)
ACID (Part 4) - Isolation (Repeatable Read)
Isolation
Obviously Jon is not the only user here, otherwise he would have ruled the Iron throne already, there are other users that concurrently liking pictures and updating the database. The question remain, how can we control what goes in first? should we go maximum isolation, stop everyone and use a first come first served approach so users don't step on each other's toes? or we should allow multiple users to update similar entries in parallel and deal with results? its our call really. First approach is slow but gives you consistent results, second approach much faster but might return incorrect results.There are four types of isolation levels that we will try to cover.
Read Uncommitted
Here there is no isolation at all; Anything that is written, whether committed or not, is available to be read. Let us see how this performs in our Instagram scenario.
Jon has already liked picture 2, but he is insisting in liking it again, we have nice atomicity and consistency that prevent him from doing so but lets see what happens. Jon fires up a like on picture 2, and fraction of a second later Sansa loads up picture 2, this will retrieve the number of likes.
Jon sends the like, first query executes successfully, incrementing the likes count.
Before Jon second query executes, Sansa's Select kicks in to read picture 2, she is going to get (2 likes). This phenomena is called a dirty read, although Jon still didn't finish his transaction, we allowed Sansa to read a dirty uncommitted entry.
Sansa issues another read to the Like table to get all the users who likes picture 2, she gets one row, which is Jon. Inconsistent with the number of likes she gets hmmm.
Jon transaction moves on and executes the second query which fails because of the constraint we have in place. Rolling back the entry for likes back to 1.
Sansa's transaction is still running she is querying other tables, doing some stuff, updating the view count perhaps, and then finally, she comes back for a final read of picture 2. She is getting a different result although she executed the same query twice in the same transaction, she got different results from each one. This phenomena is called Non-Repeatable read.
While Sansa still executing her transaction, Reek likes picture 2, its his first like so the transaction commits fine.
Finally Sansa completes her transaction by reading the likes of picture 2 again, this time she gets an extra record! what a mess. She got different set of rows running the same query. This phenomena is called Phantoms read
With read uncommitted isolation level we got all three phenomenas. The question is how important isolation for us, can we tolerate these problems?
Next post Read Committed.
-Hussein
Next post Read Committed.
-Hussein









No comments:
Post a Comment
Share your thoughts
Note: Only a member of this blog may post a comment.